Scattering by Nanoplasmonic Mesoscale Assemblies

Imran Khan

1. Introduction & Motivation

Nanoplasmonic mesoscale assemblies — dielectric microspheres coated with disordered gold nanoparticle (AuNP) shells — offer a versatile platform for tunable optical scattering, angular redistribution, and mesoscale photonic modulation.

Unlike classical Mie scattering, where a dielectric sphere produces oscillatory forward/backward lobes, the introduction of AuNPs dramatically alters the spatial distribution of scattered power. This deep dive examines how plasmonic nanoparticle coatings reshape the angular scattering profile and identifies the physical mechanisms that smooth sidelobes and enhance forward scattering.

This work is grounded in a hybrid computational framework that couples:

Method of Fundamental Solutions (MFS) for the dielectric core
Foldy–Lax multiple scattering theory for the AuNP ensemble

The combined model explicitly accounts for:

NP–NP interactions
NP–core interactions
far-field angular scattering
extinction, scattering, and absorption spectra
anisotropy and albedo

2. Physical Intuition: Why Nanoparticle Shells Reshape Angular Scattering

A bare dielectric microsphere exhibits the classical Mie like scattering pattern:

a strong forward peak
a secondary backward lobe
oscillatory sidelobes due to partial-wave interference

Adding a disordered ensemble of AuNPs immediately changes this picture.

The AuNP Shell Introduces Three Key Effects

Phase decoherence
Multiple scattering inside the shell destroys the coherent interference required to sustain sidelobes.
Absorption-driven damping
Metallic nanoparticles absorb a portion of incoming energy, reducing high-frequency oscillatory components.
Enhanced forward scattering
Plasmonic particles radiate preferentially in forward directions, especially when near a dielectric interface.

The result:

A smoother, more forward-directed angular scattering profile.

This holds true in both scattering suppression and enhancement regimes.

GitHub

schematics — Figure : Core–shell structure represented by a blue sphere (core) coated with plasmonic AuNPs (shell). The red curve shows the differential scattering cross-section of the uncoated dielectric sphere ($\sigma_{d}^{C}$), while the yellow curve represents the same dielectric core coated with AuNPs ($\sigma_{d}^{CS}$ ). The differential scattering cross-section of a plasmonic composite structure demonstrates a suppressed central lobe and smoother angular side lobes compared to the corresponding bare dielectric sphere for any particular incident wavelength.

3. Computational Model

We simulate the core–shell system using:

interior field $ \Psi^{int} $
exterior core-scattered field $\Psi^{core} $
AuNP-scattered field $ \Psi^{NP}_{n}(r) $
exciting fields $ \Psi^{E}_{n} $
incident plane wave $\Psi^{inc} $

3.1 MFS Representation of the Core

We start with a core(dielectric sphere) of radius $a$ at the origin of our coordinate system so that $|r| < a $ co rresponds to its interior , $ |r| > a $ corresponds to its exterior, and $|r|= a $ corresponds to its boundary surface. The wavenumber interion to the core is $k_{1}$ and exterion is $k_{0}$. We use the method of fundamental of solutions (MFS) to compute $\Psi^{int}$ $\Psi^{core}$. To do so, let $\hat{s}_{m}$ for $m = 1,...,M$ denotes $M$ points that sample the uting sphere so $|\hat{s}_{m}| = 1$ for $m=1,...,M$. We introduce a length $\mathcal{l} << a$ and express ,

Interior field:

\[ \Psi^{int}(r) \approx \sum_{m=1}^{M} \frac{e^{ik_{1}|r-(a+\mathcal{l})\hat{s}_{m}| }} {4\pi |r-(a+\mathcal{l})\hat{s}_{m}|}c_{m}, |r|< a \]

Hence, the evaluation of the above equation is an $\textit{exact}$ solution of

\[ \left(\nabla^{1} + k_{1}^{2}\right) \Psi^{int} = 0 \]

Similarly, exterior field:

\[ \Psi^{core}(r) \approx \sum_{m=1}^{M} \frac{e^{ik_{0}|r-(a-\mathcal{l})\hat{s}_{m}|} }{4 \pi |r-(a-\mathcal{l})\hat{s}_{m}|}b_{m}, |r| > a. \]

Thsi superposition of Green's function $\textit{exactly}$ satisfies

\[\left( \nabla^{2} + k_{0}^{2}\right) \Psi^{int} = 0 , |r| > a \]

Moreover , each Greens function satisfies the correct radiation condition for $|r|\to\infty $, so the equation above the last ensures that $\Psi^{core}$ is appropriately outgoing.

Where:

$\pm \mathcal{l}$ offsets keep sources outside their respective regions
Fibonacci sphere sampling ensures uniform collocation

3.2 AuNP Scattering Model

Each AuNP is treated as an isotropic point-scatterer:

\[\Psi_{n}^{NP}(r) = \alpha_{n} \frac{e^{ik_{0}|r-r_{n}|}}{4\pi |r-r_{n}|} \Psi^{E}_{n}, n = 1,...,N, \]

With $r_{n}$ is the center position of $\textit{nth}$ gold nanoparticles, $\alpha_{n} $ denoting its scattering amplitide, and $\Psi^{E}_{n}$ as the exciting field.

Scattering amplitude: \[ \alpha = \left[\frac{\sigma_{s}}{4\pi} - \left(\frac{k_{0}\sigma_{t}}{4\pi} \right)^{2} \right]^{1/2} + i\frac{k\sigma_{t}}{4\pi} \]

Here $\sigma_{s}$ and $\sigma_{t} $ denote the scattering and total cross-sections of the individual AuNP

This embeds:

scattering
absorption
radiation damping
optical theorem constraints

3.3 Foldy–Lax Multiple Scattering

Exciting field at NP (n):

\[ \Psi_{n}^{E} = \sum_{m=1}^{M} G_{0}(|r_{n}-(a-\mathcal{l})\hat{s}_{m}|)b_{m} + \sum_{\substack{ n^{'}=1 \\ n^{'} \neq n} }^{N} \alpha_{n^{'}} G_{0}(|r_{n}-r_{n^{'}}|)\Psi_{n'}^{E}, n = 1,...,N \]

Here $G_{0}(R)=e^{ik_{0}R} / (4\pi R)$. This yields a fully dense (N N) system.

3.4 Boundary Conditions → Block Linear System

Boundary continuity:

The field scattered by the nanoplasmonic mesoscale assembly is:

\[\Psi^{sca} = \Psi^{core} + \sum_{n=1}^{N}\Psi_{n}^{NP} \]

We relate $\Psi^{sca}$ with $ \Psi^{int}$ and the incident filed $\Psi^{inc}$ in the following way:

\[ \Psi^{inc} + \Psi^{sca} = \Psi^{int} \] and

\[ \partial_{n}\Psi^{inc} + \partial_{n}\Psi^{sca} = \partial_{n}\Psi^{int} on |r| = a \]

Resulting in the coupled system:

[ A1  A2  B1 ] [ b ] = [ f ]
[ A3  A4  B2 ] [ c ]   [ g ]
[      C    D ] [ψE]   [ 0 ]

Matrix size: (2M + N) × (2M + N).

4. Scattering Cross-Sections and Angular Metrics

4.1 Far-Field Amplitude

\[ f(\hat{o},\hat{\mathcal{i}}) = \frac{1}{4\pi} \sum_{m=1}^{M}e^{-ik_{0}(a-\mathcal{l})\hat{o}\cdot\hat{s}_{m}}b_{m}(\mathcal{i}) + \frac{1}{4\pi} \sum_{n=1}^{N}\alpha_{n}e^{-ik_{0}\hat{o}\cdot r_{n} }\Psi_{n}^{E}(\mathcal{i}) \]

4.2 Differential Cross-Section

\[ \sigma_{d}(\hat{o}, \hat{\mathcal{i}}) = |f(\hat{o},\hat{\mathcal{i}})|^{2} \]

4.3 Total Cross-Section (Optical Theorem)

\[ \sigma_{t} = \frac{4\pi}{k_{0}} Im \{f(\hat{\mathcal{i}},\hat{\mathcal{i}})\} \] , and \[ \sigma_{s} = \int_{4\pi} \sigma_{d}(\hat{o},\hat{\mathcal{i}})d\hat{o} \]

4.4 Scattering Albedo

\[ \bar{\omega}_{0} = \sigma_{s} / \sigma_{t}\]

4.5 Anisotropy Factor

\[ g = \frac{1}{\sigma_{t}}\int_{4\pi}(\hat{o}.\hat{\mathcal{i}})\sigma_{d}(\hat{o},\hat{\mathcal{i}})d\hat{o} \] The anisotropy factor($g$) gives a measure of the amount of power flow in forward/backward directions. When $g = 0$, scattering is isotropic, and when $g = \pm 1$, scattering is purely in the forward or backward directions, respectively.

5. Results & Interpretation

5.1 Scattering Efficiency

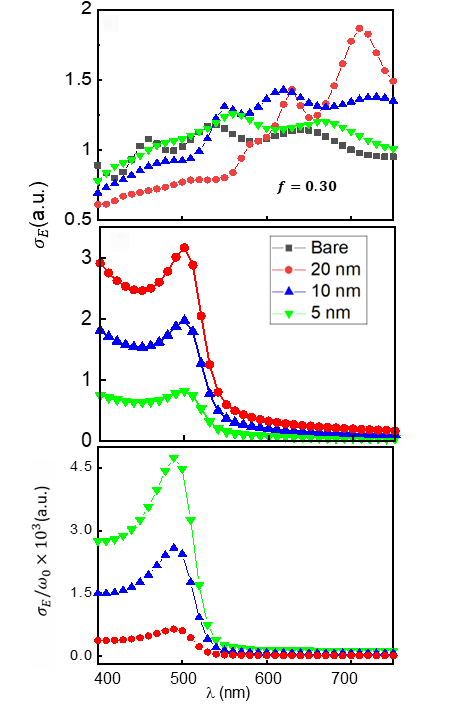
efficiencies — Figure : [Top] Scattering efficiency $\sigma_{E}$ of a 750 nm silica sphere (black square) compared with the plasmonic core–shell structures comprised of the same silica sphere acting as the core, and a concentric shell of AuNPs with a filling fraction of $f = 0.3$. [Middle] Scattering efficiency $\sigma_{E}$ of a single AuNP. [Bottom] Ratio of the extinction of a single AuNP to its respective albedo,$\sigma_{E}/\bar{\omega}_{0}$. In all plots, the diameters of the AuNPs are 20 nm (red circles), 10 nm (blue triangles), and 5 nm (green inverted triangles).

Findings:

Bare core shows strong Mie like scattering peaks
20 nm NPs suppress resonances 400–600 nm
5 nm NPs exhibit weak spectral influence

5.2 Core-Size Dependent Suppression/Enhancement

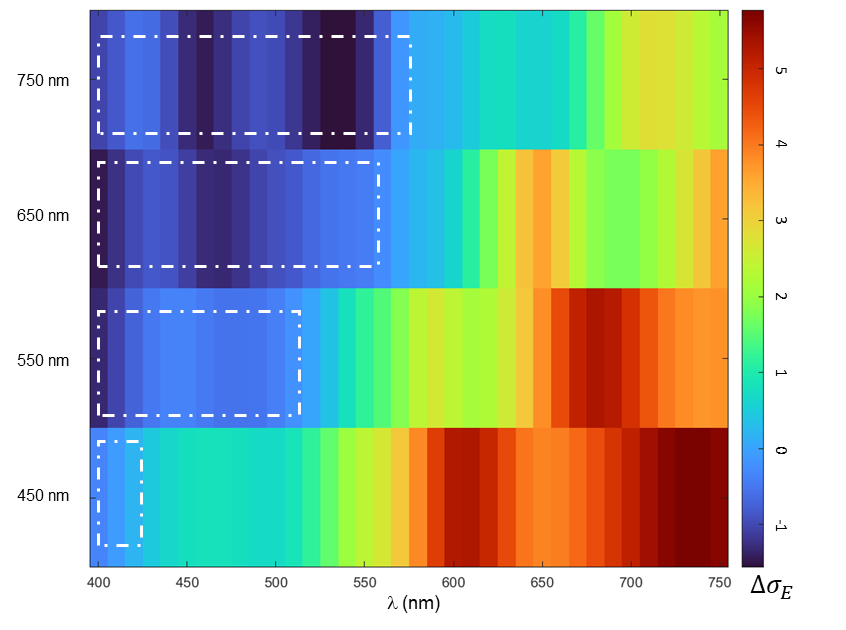
varied_cores — Figure : Comparison of $ \Delta \sigma_{E} = \sigma_{E}^{CS} - \sigma_{E}^{C}$ for varied core sizes (750, 650, 550, and 450 nm) coated with 20 nm AuNPs with a filling fraction of $f = 0.3$. The x axis gives the incident wavelength (nm) and the y axis gives the core diameters (nm). The color gradient gives the magnitude of $\Delta \sigma_{E}$ . Scattering enhancement occurs when $\Delta \sigma_{E} > 0$, and scattering suppression occurs when $\Delta \sigma_{E} < 0 $. The region of scattering suppression for each of the cores is highlighted by a dot-dashed white rectangle.

750 nm → broad suppression window
450 nm → narrow suppression, large enhancement

5.3 Differential Cross-Section: Angular Redistribution

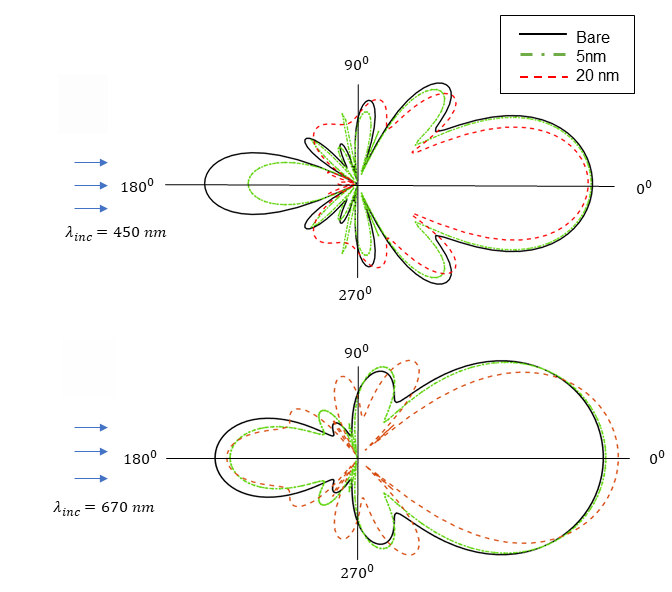
Key takeaways:

Backward lobe strongly reduced with 20 nm NP shell
Forward lobe sharpened and intensified
Angular sidelobes smoothed

This confirms phase decoherence + multiple scattering.

5.4 Henyey–Greenstein (HG) Fit

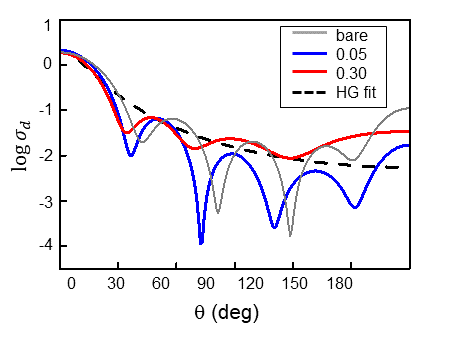
h-g fitting — Figure : Differential scattering cross-section (log-scale) of a 750 nm bare dielectric sphere (gray solid curve) with the same sphere coated with 20 nm AuNPs with filling fractions of $f = 0.05$ (solid blue curve) and $f=0.30$ (solid red curve). A fit of the Henyey–Greenstein (HG) scattering phase function to the $f = 0.3$ results is plotted as a black dashed curve.

HG model: \[\sigma_{d}^{HG} = \frac{\sigma_{s}}{4\pi} \frac{1-g^{2}}{(1+g^{2}-2g\cos\theta)^{3/2}} \]

Plasmonic coated spheres match HG extremely well.

5.5 Anisotropy

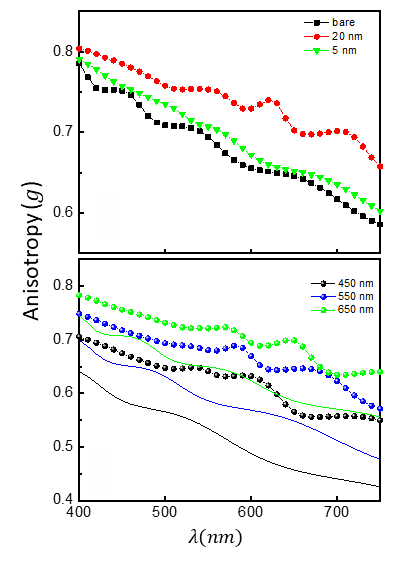
anisptropy — Figure : [Top] Anisotropy factor $g$ of a 750 nm bare dielectric core (black squares), and plasmonic core–shell structure using the same core with 20 nm AuNPs (red circles) and 5 nm AuNPs (green triangles) both with a filling fraction of $f=0.3$ over the visible spectrum. [Bottom] Anisotropy of bare cores (solid curves) and the corresponding plasmonic core–shell structures with 20 nm AuNPs with a filling fraction of $f=0.30$ (curves with circle symbols) for core diameters 450 nm (black curves) to 550 nm (blue curves), and 650 nm (green curves).

20 nm AuNP shells → highest g
Forward scattering consistently enhanced
Holds across all core sizes

6. Mechanisms Behind Angular Smoothing

6.1 Multiple-Scattering Induced Decoherence

Random AuNP distribution breaks phase alignment.

6.2 Absorption Dampens Oscillatory Features

Intrinsic AuNP absorption reduces partial-wave interference.

6.3 Forward Bias from Plasmonic Radiation

AuNPs radiate strongly forward at visible wavelengths.

7. Limitations & Future Work

Limitations

scalar wave model
no near-field coupling between NPs
O(N³) solver scaling
isotropic NP scattering assumption

Future Enhancements

full-vector Maxwell solvers
FMM acceleration
GPU-based iterative solvers
physics-informed neural surrogates

8. Applications

metasurface beam shaping
near-field imaging
forward-scattering enhancement
radiative transfer modeling
bio-photonic sensing
passive cloaking

9. Summary

This full technical deep dive demonstrates that:

AuNP shells dramatically reshape angular scattering
forward scattering is universally enhanced
absorption and multiple scattering suppress sidelobes
anisotropy increases across all core sizes
plasmonic shells can modulate both spectral and angular behavior

These findings establish nano-assembled plasmonic shells as a robust platform for mesoscale optical modulation.